“The clustering of technological innovation in time and space helps explain […] the rise and decline of hegemonic powers.”

Robert Gilpin

 

Après avoir backtesté (malheureusement sans succès) la version basique de la régression linéaire, je me sentais bien de continuer sur ma lancée Machine Learning, qui était restée un peu à la traîne comparée aux autres sections du site.

Dans cet article, nous verrons complètement autre chose que la régression linéaire. Le Machine Learning est un vaste domaine, rempli de domaines et de solutions différentes, et le sujet d’aujourd’hui est un algorithme qui me tient particulièrement à coeur : K-Means. C’était un de mes sujets d’exposé à l’école (oui j’ai eu une bonne note :)), et vous le présenter aujourd’hui, c’est un peu ma madeleine de Proust 🙂

Prérequis

Il n’y a pas de prérequis au niveau du site pour cet article. Je présente un concept nouveau, sans lien avec nos travaux précédents. Les backtests échéants seront dans un article dédié.

En revanche, il y a quelques notions mathématiques simple que l’on va utiliser et qu’il est bon de connaître, mais que je rappellerai brièvement le moment venu :

• la distance : Distance
• le point moyen : Point moyen

Clustering

Avant de décrire l’algorithme K-Means, il faut savoir que celui-ci répond à la problématique du Clustering, ou segmentation en Français.

Le Clustering est un domaine du Machine Learning / Data Mining qui fait partie de l’apprentissage non supervisé. C’est-à-dire que l’on ne va donner aucune indication sur ce que l’on recherche ou ce que l’on veut prédire / expliquer. C’est l’algorithme tout seul qui va se charger de créer des liens et des relations à partir des données, et de les associer ensemble dans un groupe : le cluster. C’est l’analyse post-opérations qui permettra de juger de la pertinence d’un cluster et comment l’exploiter.

Ce domaine est à opposer à la classification, qui elle fait parti de l’apprentissage supervisé : dans ce cas, on donne à l’algorithme des données, ainsi que la “bonne réponse”, afin que dans le futur nous puissions qualifier de nouvelles données avec cette fameuse “bonne réponse”.

Les applications du Clustering sont nombreuses et variées :

• tickets de caisses : en analysant les tickets de caisses d’un magasin, un algorithme de Clustering pourrait créer des groupes d’achats liés, et par exemple adapter une stratégie marketing
• traitement d’images : en traitement d’images, par le Clustering, il est possible d’enlever le bruit, ou regrouper les éléments d’une photo, pour les traiter indépendamment…
• immobilier : à partir de la localisation et des prix des maisons, on peut définir des zones de rentabilités pour maximiser les prospections par exemple…
• finance : on peut essayer de déterminer des clusters, et voir si les liens entre clusters permettent de fournir des signaux d’achat / vente (je ne vous cache pas que c’est cette approche qui va nous intéresser :))

Et là, ce ne sont que quelques exemples parmi les nombreux possibles.

Plus concrètement, il faut imaginer nos données comme un nuage de points à n-dimensions :

Ici on prend un exemple dans le plan, avec juste 2 dimensions. On voit au premier coup d’œil qu’il y a 2 clusters bien distincts, et le but de notre algorithme va être de les mettre en évidence.

L’algorithme K-Means

L’algorithme K-Means, en Français K-moyennes est l’algorithme de base pour répondre à ce problème.

Il a pour paramètre le nombre de clusters que l’on trouver : K (d’où le nom K-Means)

A chacun de ces clusters est associé le centre du cluster, qui est le point moyen (d’où le nom K-Means encore une fois :)) des points appartenant au cluster. Etant donné qu’au début aucun point de donnée n’est associé à un cluster, on les place comme on veut.

Et c’est un algorithme itératif :

• à chaque itération, on associera chaque point de donnée au cluster dont le centre est le plus proche.
• une fois que tous les points ont leur nouveau cluster, on met à jour les centres des clusters, qui auront bougé si certains points ont changé de clusters
• on continue jusqu’à ce que les centres des clusters ne bougent plus

Il faut enfin définir la distance. J’ai dit qu’un point était associé au cluster dont le centre est le plus proche. La distance utilisée dépend donc de vos données. Pour les tickets de caisse, ça pourrait être la probabilité d’apparition d’un article sachant qu’un autre article est là… Pour le traitement d’images, ça peut être la différence de couleurs d’un pixel donné… A chaque problématique sa distance. Pour notre exemple en 2D, on utilisera la distance Euclidienne, qui est aussi la norme du vecteur entre les 2 points :

Distance = Racine_carrée ( ( Xb – Xa )² + ( Yb – Ya )² )

En pseudo code ça nous donne :

 
#data = notre jeu de donnée
#K = nbre de clusters

#initialisation des centres
centers = list()
pour i = 1 à K
  centers.Add(new Point(Hasard(), Hasard()) # Point { X, Y }

clusters = new int[data.Size] # résultat contenant le cluster associé à chaque point
erreur = 1 #condition d'arrêt de l'algo

tant que error > 0
{
    centers_copy = hardcopy ( centers ) # fait une copie exacte des données, pas des références
    
    pour tout (element dans data)
    {
      # je m'autorise les opérations vectorielles pour simplifier
      distances = Distance ( element * centers ) # Distance Euclidienne pour la 2D

      # arg min renvoie l'indice du minimum d'un tableau, représentant mon cluster ici
      clusters[element] = arg_min(distances) 
    }

    # mise à jour des centres
    pour i = 1 à K
      centers[i] = point_moyen ( data[x => clusters[x] == i] )

    # error = 0 si tous les centres sont les même qu'à l'itération précédente
    error = Distance ( centers, centers_copy )
}

Il ne reste plus qu’à voir le déroulement en live !

Implémentation

Ceci n’a pas été fait le GoingStrikerBot à proprement parler, mais dans des outils que j’ai implémenté en complément pour me permettre de faire des POC, études de sujet… J’ai utilisé exactement les même points que dans l’image du début. Voici le fichier correspondant : K-Means example file

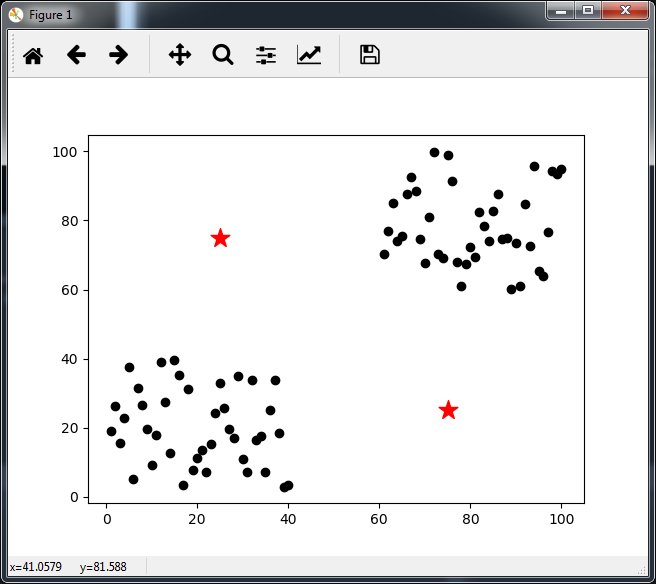
Ceci est notre point de départ. J’ai choisi 2 clusters comme paramètre de l’algo (incroyable :)). Les étoiles correspondent aux centres des clusters à l’initialisation. J’ai fait exprès de les choisir complètement hors des clusters pour vous montrer qu’ils convergeront quand même.

1ère itération :

Il y a un cluster bleu, et un cluster vert. Avec les points de départs des centres, à la première itération, il a séparé les points selon une diagonale croissante, alors qu’on aurait pu croire qu’il aurait trouvé facilement les clusters finaux ! (comment ça j’ai fait exprès de choisir les centres initiaux ? :)) On remarque également le léger déplacement des centres vers le milieu du graphique.

On repart pour un tour :

Les clusters commencent à vraiment se démarquer, avec encore quelques points rebels. En revanche, les centres ont clairement déviés vers les clusters. Suite et fin :

Avec les centres aussi proches des amas de points à la dernière itération, il était assez évident que les clusters finaux seraient détectés cette fois.

Et c’est fini. En 3 itérations, l’algorithme a réussi à détecter les 2 clusters présents dans notre exemple. L’exemple était très basique, et dans la vraie vie, les problèmes sont plus complexes que ça. Néanmoins, maintenant que vous connaissez le principe de la méthode, nous allons pouvoir tenter de l’exploiter et voir si ça a un intérêt niveau modèle et stratégie ! Keep tuned ! 🙂